Mathematical Cryptography I

Simple substitution ciphers

Simple substitution ciphers are a foundational cryptographic method where each letter in the plaintext is replaced by a letter from a shuffled alphabet. This method is straightforward yet introduces the basic concept of encrypting a message to make it unreadable to unintended recipients.

How It Works

• The cipher operates by creating a one-to-one mapping between the standard alphabet and a mixed alphabet. Each letter from the plaintext is substituted according to this mapping to produce the ciphertext.

• For instance, if the letter 'A' maps to 'L', 'B' to 'M', and so on, the word "HELLO" might be encrypted as "XYZZY" given a specific mapping.

Historical Context: The Caesar Cipher

• Caesar cipher is an early form of simple substitution cipher. In a Caesar cipher, the alphabet is shifted a fixed number of places. For example, with a shift of three, 'A' becomes 'D', 'B' becomes 'E', and so forth.

• This cipher is named after Julius Caesar, who is historically noted to have used it for confidential communications.

Vulnerabilities: Frequency Analysis

• A significant part of the discussion on simple substitution ciphers involves their vulnerability to frequency analysis. This method of cryptanalysis leverages the fact that certain letters and combinations of letters appear more frequently than others in a given language.

• For example, in English, 'E' is the most common letter, and pairs like 'TH' are common bigram. By analyzing the frequency of letters and letter pairs in the ciphertext, a cryptanalyst can begin to deduce the original mappings and decrypt the message.

Despite their vulnerability, simple substitution ciphers played a crucial role in the early development of cryptographic methods. They introduced the principle of altering plaintext to secure its contents, laying the groundwork for more complex and secure ciphers. The ease with which these ciphers can be broken underscores the need for advancements in cryptographic techniques, leading to the development of more sophisticated encryption algorithms.

Divisibility

At its core, the concept of divisibility is straightforward yet powerful. An integer b is said to divide another integeraif there exists an integer c such that a = bc.

Ex: We have 847 | 485331, since 485331 = 847 · 573. On the other hand, 355 !/ 259943, since when we try to divide 259943 by 355, we get a remainder of 83. More precisely, 259943 = 355 · 732 + 83, so 259943 is not an exact multiple of 355.

This simple relationship forms the backbone of much more complex mathematical structures encountered in cryptography.

Greatest Common Divisor (GCD)

The greatest common divisor of a and b is, as its name suggests, the largest positive integerdsuch thatd | aandd | b. The greatest common divisor of a and b is denoted gcd(a, b). If there is no possibility of confusion, it is also sometimes denoted by (a, b). If a and b are both 0, then gcd(a, b) is NOT DEFINED.

Ex: Calculation of gcd (748, 2024)

Not Efficient Approach: Making lists of all the positive divisors of 748 and of 2024.

Divisors of 748 = {1, 2, 4, 11, 17, 22, 34, 44*, 68, 187, 374, 748},*

Divisors of 2024 = {1, 2, 4, 8, 11, 22, 23, 44*, 46, 88, 92, 184, 253, 506, 1012, 2024}.*

Efficient Approach: Division with remainder, which is simply the method of “long division”. Thus, if a and b are positive integers and if you attempt to divide a by b, you will get a quotient q and a remainder r, where the remainder r is smaller than b.

Finding GCD with Division

1. According to the definition, we can say a = bq + r and 0 ≤ r < b. The values q and r are unique for given a and b.

2. Start by dividing a by b to get the remainder r. Any common divisor of a and b is also a divisor of r, and any common divisor of b and r is a divisor of a. This means the GCD of a and b can be equated to the GCD of b and r. So;

   gcd(a, b) = gcd(b, r)

3. Repeat the process, dividing b by r to get another quotient and remainder, reducing the remainder each time until r = 0. The final value gcd(s, 0) = s is equal to the gcd(a, b).

We illustrate with an example and then describe the general method, which goes by the name Euclidean algorithm.

2024 = 748 · 2 + 528

748 = 528 · 1 + 220

528 = 220 · 2 + 88

220 = 88 · 2 + 44 ⇾ gcd(2024, 748) = 44

88 = 44 · 2 + 0

The Euclidean Algorithm

Let a and b be positive integers with a ≥ b. The following algorithm computes gcd(a, b) in a finite number of steps.

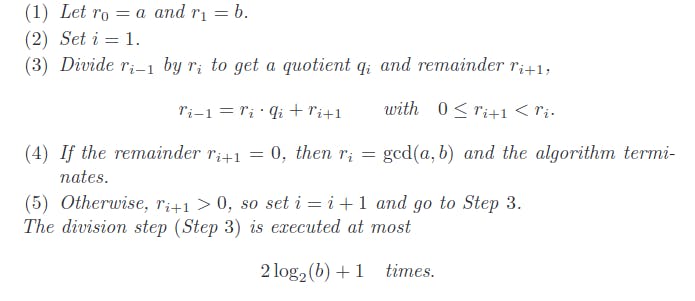
The Discrete Logarithm Problem

The DLP arises in the context of finite fields, particularly Fp​, which is a field with a prime number of elements p. For a given prime p and a primitive element g in Fp​, the DLP involves finding an exponent x such that:

g ^ x ≡ h ( mod p )

Here, g is a primitive root for Fp​, and h is a nonzero element of Fp​. The exponent x that satisfies this equation is known as the discrete logarithm of h the base g, denoted by;

Mathematical Representation

• Primitive Element g: A primitive element g of Fp​ is such that every nonzero element of Fp​ can be expressed as a power of g. By Fermat's little theorem;

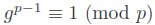
and no smaller power of g equals 1.

• Discrete Logarithm x: The discrete logarithm problem seeks the integer x satisfying;

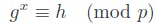
• If such an x exists, there are actually infinitely many solutions, since;

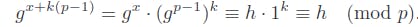
for any integer k, due to the periodic nature implied by Fermat’s little theorem.

The discrete logarithm x is thus defined modulo p−1, acknowledging the cyclic nature of the powers of g in Fp​.

Diffie-Hellman Key Exchange

Alice and Bob need to securely share a secret key over an insecure channel monitored by Eve. Diffie and Hellman proposed using the discrete logarithm problem's complexity as a possible solution to this challenge.

Mathematical Representation of the Algorithm

1. Public Parameter Creation

Alice and Bob start by choosing a large prime numberp and a nonzero integergmodulop and share them in public.

2. Private Computations

Next, Alice selects a secret integer a, and Bob chooses a secret integer b. They use their secret integers to compute:

3. Public Exchange of Values

Alice sends to Bob ⇾ A,

Bob sends to Alice ⇾ B

4. Further Private Computations

Bob and Alice again use their secret integers to compute:

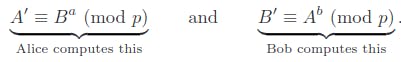
The values that they compute are the same. (A′ = B′)

Current guidelines suggest that Alice and Bob choose a prime p having approximately 1000 bits (i.e., p ≈ 21000) and an element g whose order is prime and approximately p/2. Then Eve will face a truly difficult task. However, Eve can solve the DLP (Discrete Logarithm Problem), then she can compute Alice and Bob’s secret exponents a and b from the intercepted values A and B, and then it is easy for her to compute their shared key gab. (Needs to compute only one of a and b.) But the converse is less clear. Suppose that Eve has an algorithm that efficiently solves the DHP (Diffie-Hellman Problem). Can she use it to also efficiently solve the DLP?

The ElGamal Public Key Cryptosystem

Although Diffie-Hellman algorithm provides a method of publicly sharing a secret random key, it does not enough to being a public key cryptosystem. The most natural development of a public key cryptosystem following the Diffie–Hellman is a system described by Taher ElGamal in 1985. The ElGamal public key encryption algorithm is based on the DLP and is closely related to Diffie–Hellman key exchange.

Mathematical Representation

1. Public Parameter Creation

A trusted party chooses and publishes a large prime p and an element g (instead of Alice and Bob) modulo p of large (prime) order.

2. Key Creation

2.1 Alice chose private key 1 =< a =< p-1.

2.2 Computes A = g ^ a (mod p).

2.3 Alice publishes the public key A.

3. Encryption

3.1 Bob chooses plaintext m.

3.2 Bob chooses random temporary key k.

3.3 Uses Alice's public key A to compute c1 = g ^ k (mod p)

and c2 = m A^k (mod p).

3.4 Bob sends ciphertext (c1, c2) to Alice.

4. Decryption

Alice compute m with:

How hard is the DLP ?

The discrete logarithm problem is a bit like solving a puzzle, where you need to figure out a special number, called an exponent. Imagine you have a specific operation you can do with numbers, and you want to find out how many times you need to repeat this operation on a base number g to get another number h. This is tough because you have to guess and check a lot of possibilities, especially when the numbers involved are massive.

1. Guess and Check - Not Practical

   If you tried to solve this by simply trying every single possibility one by one, you might end up trying an enormous number of times, especially if the range of possible numbers is huge.

2. Fast Exponentiation - Still Not Practical

   This method starts to feel slow when the numbers get really large, because you still have to do a lot of guesses.

Shanks's BabyStep-GiantStep Algorithm

This method is designed to solve the DLP more efficiently than simply trying brute force.

How it works ?

1. Divide and Conquer

Create a 2 smaller list of possibilities.

Find the exponent x solves the DLP equation.

2. Setting Up Lists

Baby Steps: Store the powers of g in a list. (g, g^2, g^3, ...)

Giant Steps: Calculate powers of h multiplied by inverse powers of g raised to large increments and store them in another list. (h.g^-n, h.g^-2n, ...)

3. Finding a match

Looks for a common element between two lists.

• "Finding a common element" means two calculation methods agree, revealing the solution x. (collision)

4. Efficiency

This method significantly reduces the number of operations compared to brute force.

In a group of size 10,000, Shanks's Algorithm needs only around 200 steps to find the answer (200^2 = 10.000) but a brute force would require all 10,000 options.

The Chinese Remainder Theorem (CRT)

Imagine you're trying to figure out a number that, when divided by 3, leaves a remainder of 2, and when divided by 5, leaves a remainder of 1. Doing this by checking each number one by one is so boring and requires a lot of time. The CRT exists to solve this kind of problem quickly and efficiently by finding a number that works for all conditions(aka puzzles) without having to test every single possibility.

Simple Example:

Puzzle 1: Event that occurs every 7 days (weekly on a Monday), and today is Monday. Today could be represented as:

x = 0 (mod 7)

Puzzle 2: A second event that happens every 5 days, and today it's happening too. Today could be represented as:

x = 0 (mod 5)

What are the days that both events will happen again on the same day?

CRT comes to play

The CRT tells that both events will align every 7×5=35 days. So, the next time both events happen on the same day will be 35 days from today.

Mathematical Representation

Looking for an integer x that simultaneously solves both of the puzzles

below:

• x = 1 (mod 5)

• x = 9 (mod 11)

For the first puzzle, we can say:

x = 1 + 5y (y ∈ Z)

For the second one;

x = 1 + 5y = 9 (mod 11) then, 5y = 8 (mod 11)

Finding modulo inverse:

(a x b = 1 (mod m))

To solve 5y = 8 (mod 11), we need the inverse of 5 modulo 11. This inverse exists because gcd(5, 11) = 1.

5 x b = 1 (mod 11).

Because the modulus is so small that we can find it by trial and error.

5x9 = 45 = 1 (mod 11)

9 is the modular inverse of 5 modulo 11.

Using the Inverse to Solve for y:

Given the equation above:

5y = 8 (mod 11)

Multiply Both Sides by the Inverse of 5 Modulo 11:

Multiply both sides of the equation by 9:

9×5y = 9×8 (mod 11)

Simplify the Equation & Solving y:

Because 9 x 5 = 1 (mod 11), the equation simplifies

y = 72 (mod 11) ⇾ y

Finding x with y:

Since;

x = 1 + 5y

1 + 5x6 = 31

Solving puzzles with composite moduli

Let's find x such that: x^2 = 197 (mod 437)

(437 is a composite number because 437 = 19 × 23. Both 19 and 23 are prime numbers.)

Step 1.

Factor the modulus

437 = 19 × 23

Step 2.

Apply CRT

Since 437 can be factored into two relatively prime numbers, we can split the original congruence into two separate congruences based on these prime factors:

1. x^2 = 197 = 7 (mod19)

2. x^2 = 197 = 13 (mod 23)

Step 3.

Simplify the Congruences

1. x^2 = 7 (mod 19) and x^2 = 197 = 13 (mod 23)

Because 19 (mod4) = 3, 23 (mod  4)=3;

x^2 = 64 ⇾ x = 8 | -8

x^2 = 36 ⇾ x = 6 | -6

Step 4 with choosing positive solutions 8 and 6.

Apply the CRT Again

x = 8 (mod 19) and x = 6 (mod 23);

Inverse modulo of 6 and 23:

x = 23k + 6 = 8 (mod 19)

23k = 2 (mod 19)

k = 5

Multiply both sides of equation with 5:

5 x 23k = 2 x 5 (mod 19) ⇾ k = 10

Finally:

x = 23 x 10 + 6 = 236 | - 236 for x^2 = 197 (mod 437) equation.

If the modulus were prime, there would be only these "two" square roots. However, since 437 = 19 · 23 is composite, there are two others. In order to find them, we replace one of 8 and 6 with its negative. This leads to the values x = 144 and x = 293.

This means that 197 has 4 square roots modulo 437.

References

An Introduction to Mathematical Cryptography

The Discrete Logarithm Problem

The Euclidean Algorithm